In this article we will discuss the steps and intuition for calculating the inverse of a matrix and show examples using Python.
Table of contents
Introduction
The inverse of a matrix is an important concept in linear algebra. It is often seen in many equations and the simplest use case for it is helping find the solution of a system of linear equations though inversing a matrix.
We already know what a matrix represents, so now we can take a look at what is its inverse and how to calculate it.
To continue following this tutorial we will need the following Python library: numpy.
If you don’t have them installed, please open “Command Prompt” (on Windows) and install them using the following code:
pip install numpy
Inverse matrix explained
We already know what a matrix is and understand the use cases for it in linear algebra. So what is an inverse matrix?
Inverse of a matrix defined
Let’s take a step back and and think about numbers. You can pick any number, for example \(5\). Can we find an inverse of 5? Yes! It’s simply its reciprocal, which is \(\frac{1}{5}\), which we also write as: \(5^{-1}\).
What is so unique about it? If you multiply a number by it’s inverse, your equation will be equal to \(1\):
$$5 \times 5^{-1} = 1$$
Matrices work in a similar way. Consider we have some 2×2 matrix \(A\):
$$A = \begin{bmatrix} 3 & 7 \\ 2 & 5 \end{bmatrix}$$
and a 2×2 identity matrix \(I\):
$$I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$$
We would think that there exists an inverse matrix \(A^{-1}\), such that:
$$A \times A^{-1} = I$$
or in our case:
$$\begin{bmatrix} 3 & 7 \\ 2 & 5 \end{bmatrix} \times A^{-1} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$$
When does an inverse of a matrix exist?
But it turns out that the inverse matrix may not always exist! The inverse matrix of matrix \(A\) exists if and only if two of the below conditions are satisfied:
- Matrix \(A\) is a square matrix (2×2, 3×3, and so on) where the number of rows equals to the number of columns
- The determinant of matrix \(A\) is not equal to zero: \(det(A)\neq 0\)
Inverse of a 2×2 matrix
In our example we are working with a 2×2 matrix, whose determinant is equal to:
$$det(A) = 3 \times 5 – 7 \times 2 = 1 \neq 0$$
Then how do we actually get the inverse matrix \(A^{-1}\)?
In case of a 2×2 matrix it’s quite simple:
$$\begin{bmatrix} a & b \\ c & d \end{bmatrix}^{-1} = \frac{1}{ad-bc} \times \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}$$
In our example:
$$A^{-1} = \begin{bmatrix} 3 & 7 \\ 2 & 5 \end{bmatrix}^{-1} = \frac{1}{(3 \times 5) – (7 \times 2)} \times \begin{bmatrix} 5 & -7 \\ -2 & 3 \end{bmatrix} = \begin{bmatrix} 5 & -7 \\ -2 & 3 \end{bmatrix}$$
Now we found the inverse of matrix \(A\)!
How can we check that it works?
Recall:
$$A \times A^{-1} = I$$
We can use matrix multiplication to check our result:
$$\begin{bmatrix} 3 & 7 \\ 2 & 5 \end{bmatrix} \times \begin{bmatrix} 5 & -7 \\ -2 & 3 \end{bmatrix} = \begin{bmatrix} (3 \times 5) + (7 \times (-2)) & (3 \times (-7)) + (7 \times 3) \\ (2 \times 5) + (5 \times (-2)) & (2 \times (-7)) + (5 \times 3) \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$$
We have correctly calculate the inverse of a 2×2 matrix \(A\)!
We can also think about it graphically.
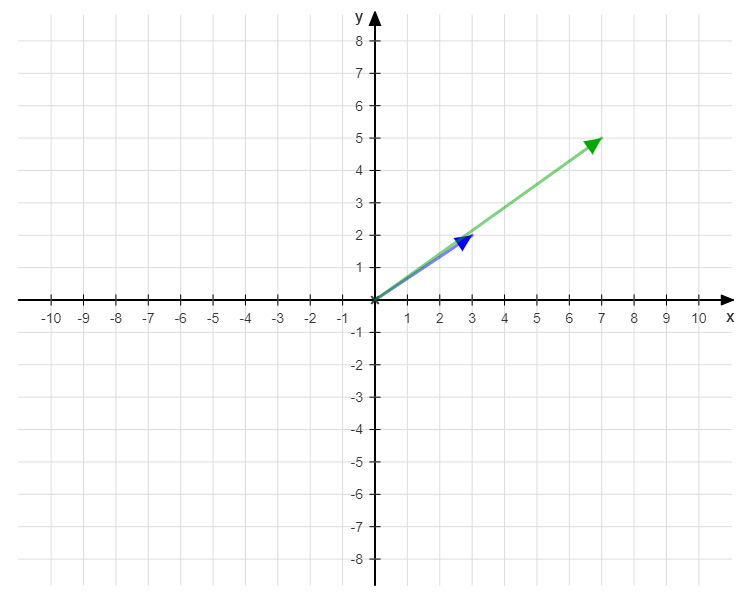
Let’s can represent matrix \(A\) in cartesian space, where the columns of the matrix become vectors:
$$\vec{a}_1 = (3, 2)$$
$$\vec{a}_2 = (7, 5)$$
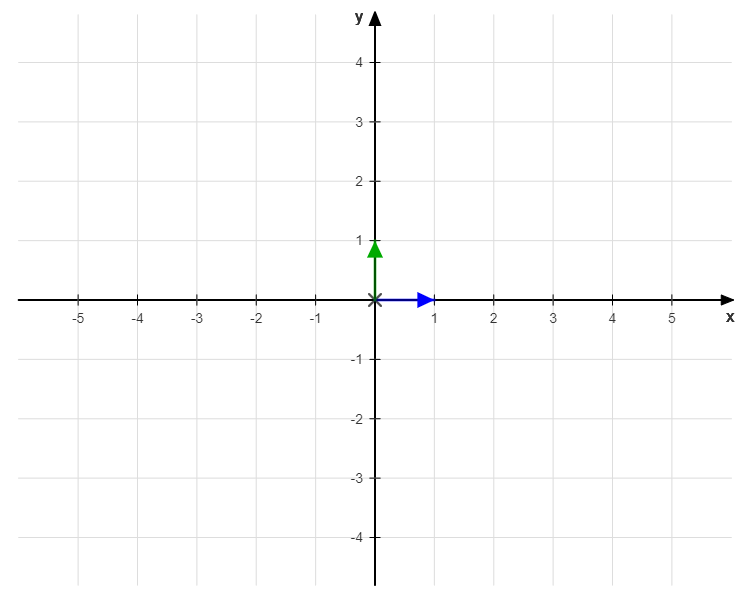
And also represent the identity matrix in cartesian space, which are simply the base vectors:
$$\vec{i}_1 = (1, 0)$$
$$\vec{i}_2 = (0, 1)$$
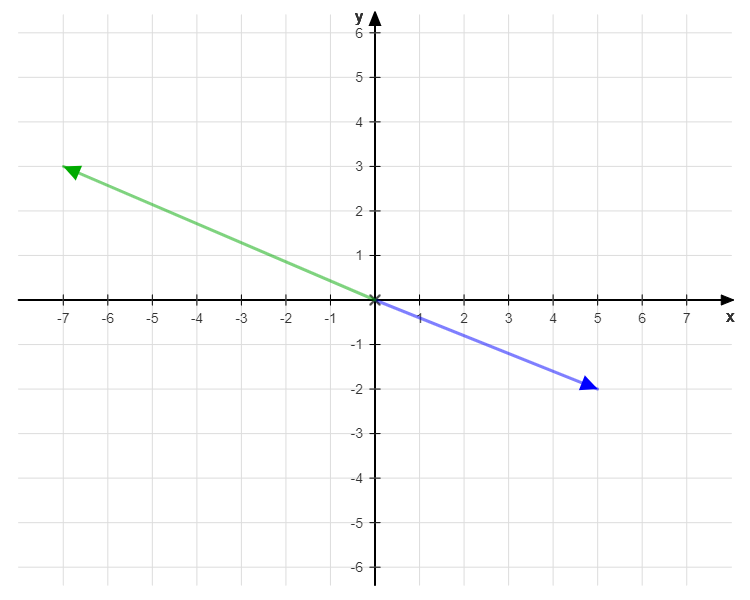
Following this logic, the inverse matrix will also be represented by some vectors, and they are such that if we multiply matrix \(A[/latex ([latex]\vec{a}_1, \vec{a}_2 \)) by vectors of its inverse matrix \(A^{-1}\) (let’s call them: \(\vec{inv}_1, \vec{inv}_2 \)), the result should be the base vectors (\(\vec{i}_1, \vec{i}_2 \)) which represent the identity matrix \(I\).
Since we already calculate the inverse matrix \(A^{-1}\), the resulting vectors are:
$$\vec{inv}_1 = (5, -2)$$
$$\vec{inv}_2 = (-3, 7)$$
Inverses of larger matrices
Now, it is as simple to calculate the inverse for a large matrix like 3×3 or 5×5? Not really. As the size of the matrix increases, the complexity in a sense of numbers of steps also increases!
There are a few examples of calculations of inverses of larger matrices like 3×3 and 5×5 using Gaussian elimination which you can find online.
In general, for larger size matrices we prefer to have access to technology like Python to allows us to get the results in a quick and efficient way.
Inverse of a matrix in Python
In order to calculate the inverse matrix in Python we will use the numpy library. And the first step will be to import it:
import numpy as np
Numpy has a lot of useful functions, and for this operation we will use the linalg.inv() function which computes the inverse of a matrix in Python.
Recall that in Python matrices are constructed as arrays. And the next step will be to define the input matrices. We are going to use the same 2×2 matrix as in the example from the previous section:
A = np.array([[3, 7],
[2, 5]])
Now that we have the required matrix, we can easily calculate its inverse:
A = np.array([[3, 7],
[2, 5]])
A_inv = np.linalg.inv(A)
print(A_inv)
And you should get:
[[ 5. -7.]
[-2. 3.]]which is exactly the same output as in our example where we calculated it manually.
We can also check it it’s correct by using matrix multiplication in Python:
I = np.matmul(A, A_inv)
print(I)
And you should get:
[[ 1.00000000e+00 -1.77635684e-15]
[ 0.00000000e+00 1.00000000e+00]]which are the top right value is almost zero (numpy issue), but it is an identity matrix just like \(I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\)
Conclusion
In this article we discussed the intuition behind matrix inversion using a linear algebra approach, as well as shown a complete example using Python.
Feel free to leave comments below if you have any questions or have suggestions for some edits and check out more of my Linear Algebra articles.
