In this article we will discuss the steps and intuition for creating the identity matrix and show examples using Python.

Table of contents

Introduction

The identity matrix (\(I\)) is often seen in a lot of matrix expressions in linear algebra, and is a special case of a diagonal matrix.

At this point you should be familiar with what a matrix represents as it will be useful to understand the meaning behind the identity matrix.

To continue following this tutorial we will need the following Python library: numpy.

If you don’t have them installed, please open “Command Prompt” (on Windows) and install them using the following code:


pip install numpy

Identity matrix explained

We already know what a matrix is, but what exactly is an identity matrix and how is it being used?

The identity matrix \(I_n\) is a square matrix of order \(n\) filled with ones on the main diagonal and zeros everywhere else.

Here are a few examples:

$$I_1 = \begin{bmatrix} 1 \end{bmatrix}$$

$$I_2 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$$

$$I_3 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

and so on for the larger dimensions.

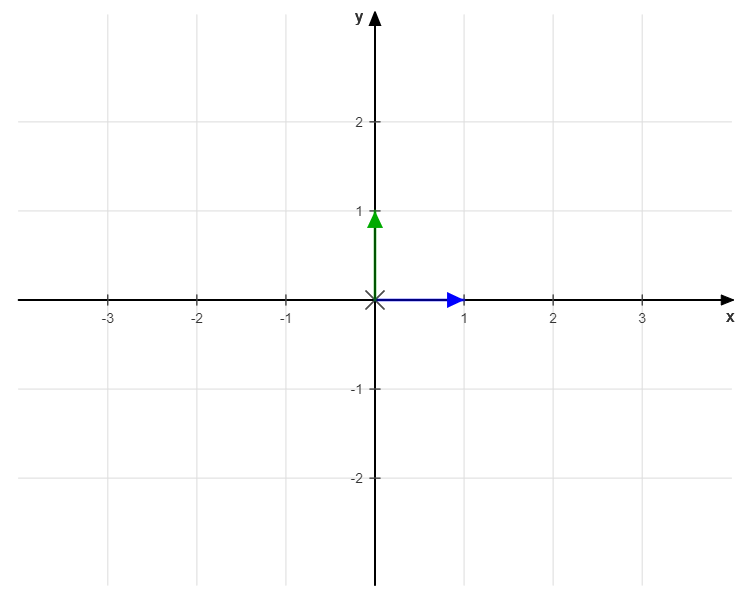
Graphically, the \(I_2\) matrix simply represents the base vectors:

$$\vec{i}_1 = (1, 0)$$

$$\vec{i}_2 = (0, 1)$$

Identity matrix properties

Here are some useful properties of an identity matrix:

  1. An identity matrix is always a square matrix (same number of rows and columns), such as: 2×2, 3×3, and so on.
  2. The result of multiplying any matrix by an identity matrix is the matrix itself (if multiplication is defined)
    $$A \times I = A$$
    $$\begin{bmatrix} 3 & 7 \\ 2 & 5 \end{bmatrix} \times \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 3 & 7 \\ 2 & 5 \end{bmatrix}$$
  3. The result of multiply a matrix by its inverse matrix is the identity matrix
    $$A \times A^{-1} = I$$
    $$\begin{bmatrix} 3 & 7 \\ 2 & 5 \end{bmatrix} \times \begin{bmatrix} 5 & -7 \\ -2 & 3 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$$

Identity matrix in Python

In order to create an identity matrix in Python we will use the numpy library. And the first step will be to import it:


import numpy as np

Numpy has a lot of useful functions, and for this operation we will use the identity() function which creates a square array filled with ones in the main diagonal and zeros everywhere else.

Now let’s create a 2×2 identity matrix:


I = np.identity(2)

print(I)

And you should get:

[[1. 0.]
 [0. 1.]]

Now you know how to create an identity matrix and can further explore matrix operations by calculating matrix inverses and multiplying matrices in Python.

Conclusion

In this article we discussed the steps and intuition for creating the identity matrix, as well as shown a complete example using Python.

Feel free to leave comments below if you have any questions or have suggestions for some edits and check out more of my Linear Algebra articles.