In this article we will discuss how to solve a quadratic equation using Python.

Table of Contents

Introduction

In algebra, quadratic equations are widely used in a lot of tasks. A quadratic equation (second-degree polynomial) always has a squared term which differentiates it from our usual linear equations.

In this tutorial we will use the math library (prebuilt in Python) for solving quadratic equations using Python

We will also need numpy to work with arrays, and matplotlib to plot the graph of the quadratic equation using Python.

If you don’t have it installed, please open “Command Prompt” (on Windows) and install it using the following code:


pip install numpy
pip install matplotlib

Quadratic formula

We begin with understanding the standard form of quadratic equation:

$$ax^2 + bx + c = 0$$

where a, b, c are real numbers and \(a \neq 0\).

So how do we know if the equation has a solution? And if it does, how many solutions?

Solve quadratic equation

Step 1: Calculate discriminant

The first step to solve a quadratic equation is to calculate the discriminant. Using simple formula:

$$D = b^2 – 4ac$$

we can solve for discriminant and get some value. Next, if the value is:

  • positive, then the equation has two solutions
  • zero, then the equation has one repeated solution
  • negative, then the equation has no solutions

Step 2: Solve for x values

To solve for each x value, we use the following quadratic formula:

$$x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} = \frac{-b \pm \sqrt{D}}{2a}$$

which means that:

$$x_1 = \frac{-b + \sqrt{D}}{2a}$$

$$x_2 = \frac{-b – \sqrt{D}}{2a}$$

and these are all the steps we need to take to find the solution for the quadratic equation.

Solve quadratic equation (Example)

As an example, let’s consider the following quadratic equation:

$$x^2 – 5x – 14 = 0$$

where \(a = 1\), \(b = -5\), and \(c = -14\).

As the first step, we will calculate the discriminant:

$$D = b^2 – 4ac = (-5)^2 – 4 \times 1 \times (-14) = 81$$

Since \(D > 0\), this equation will have two roots.

Let’s calculate \(x_1\) and \(x_2\):

$$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-(-5) + \sqrt{81}}{2 \times 1} = 7$$

$$x_2 = \frac{-b + \sqrt{D}}{2a} = \frac{-(-5) – \sqrt{81}}{2 \times 1} = -2$$

The solution for this equation is: \(x_1 = 7\) and \(x_2 = -2\)

Solve quadratic equation using Python

As an example, let’s consider the following quadratic equation:

$$x_1 – 5x_2 – 14 = 0$$

where \(a = 1\), \(b = -5\), and \(c = -14\).

Step 1: Get user input for equation coefficients (a , b, c)

First, we need to get these coefficients entered by the user:


a, b, c = eval(input("Please enter the a, b, c coefficients of your quadratic equation: "))

Here we will need to pass the three comma-separated values as: 1,-5,-14.

Clearly, if you pass anything other than a real number (string or boolean), it won’t break the input function but further calculations won’t work. To prevent this, you should consider adding a set of checks to validate the user input:


check_input = True
while check_input:
    a, b, c = eval(input("Please enter the a, b, c coefficients of your quadratic equation: "))
    try: 
        float(a), float(b), float(c)
        check_input = False
    except ValueError:
        print("Please make sure the coefficients are real numbers and try again")
        check_input = True

So far we created the a, b, and c variables in Python.

Step 2: Calculate discriminant using Python

Next we will calculate discriminant. We will need to use the math library (prebuilt in Python) to use the square root function:


from math import sqrt

disc = b*b-4*a*c

For the values we entered above, the discriminant value should be 81.

Step 3: Find roots of quadratic equation using Python

And finally we solve for the roots of the equation. Recall that we also need to check if the discriminant is less than zero, then the quadratic equation has no solutions:


if disc >=0:
    x1 = (-b+sqrt(disc))/(2*a)
    x2 = (-b-sqrt(disc))/(2*a)
    print("The roots of the equation are:", x1, x2)
else:
    print("The equation has no solutions")

For our example we should get \(x_1 = 7\) and \(x_2 = -2\).

Plot quadratic function using Python

The graph representation of a quadratic equation is a parabola.

When the quadratic equation is simplified to be equal to zero, the roots of the equation are the y-axis intercepts.

Let’s plot the quadratic equation from the previous section using Python and see where the roots of the equation are located.

We begin by importing the required libraries:


import matplotlib.pyplot as plt
import numpy as np

Next let’s determine the \(x\)-axis range we would like to consider. For this example, let’s take a range between -10 and 15:


x = np.linspace(-10, 15)

And we can have our function for \(y\) using the parameters from the previous section:


y = x**2 - 5*x - 14

First we will plot the x-axis and y-axis as dashed lines along with the axis labels:


plt.hlines(y=0, xmin=min(x), xmax=max(x), linestyles='dashed')
plt.vlines(x=0, ymin=min(y), ymax=max(y), linestyles='dashed')
plt.xlabel('x')
plt.ylabel('y')

And then plot the parabola:


plt.plot(x, y)
plt.show()

And you should get:

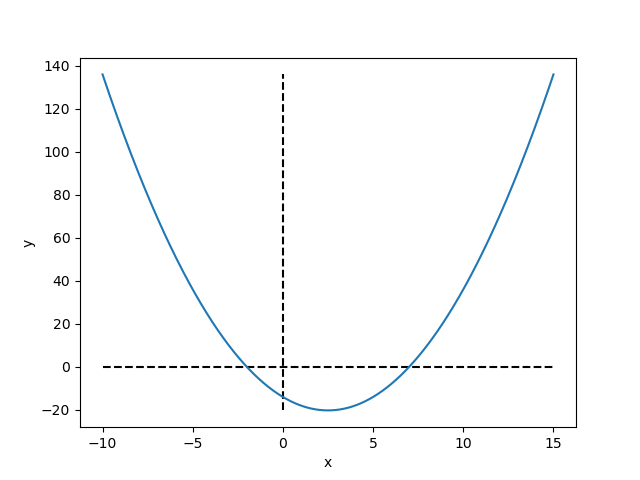
plot quadratic function python

On the graph above you can see that points (-2, 0) and (7, 0) are the x-axis intercepts which are also the roots of the quadratic equation.

Program to solve quadratic equations using Python


from math import sqrt

check_input = True
while check_input:
    a, b, c = eval(input("Please enter the a, b, c coefficients of your quadratic equation: "))
    try: 
        float(a), float(b), float(c)
        check_input = False
    except ValueError:
        print("Please make sure the coefficients are real numbers and try again")
        check_input = True

disc = b*b-4*a*c

if disc >= 0:
    x1 = (-b+sqrt(disc))/(2*a)
    x2 = (-b-sqrt(disc))/(2*a)
    print("The roots of the equation are:", x1, x2)
else:
    print("The equation has no solutions")

Conclusion

In this article we covered how you can solve a quadratic equation using Python and math library.

Feel free to leave comments below if you have any questions or have suggestions for some edits and check out more of my Optimization articles.