In this article we will explore trigonometric functions in Python.
Table of contents
- Introduction
- Sine function
- Inverse sine function
- Cosine function
- Inverse cosine function
- Tangent function
- Inverse tangent function
- Conclusion
Introduction
Since this tutorial is focused on trigonometric functions, we will need to have a few important definitions to better understand each function.
Trigonometry
Trigonometry is a branch of mathematics that studies relationships between angles and lengths of sides in triangles.
The three main trigonometric functions used in trigonometry are: sine, cosine, and tangent, which are based on the right triangle.
Right Triangle
What is a right triangle? It’s a triangle with a right angle (or \(90^{\circ}\) angle).
See example below:
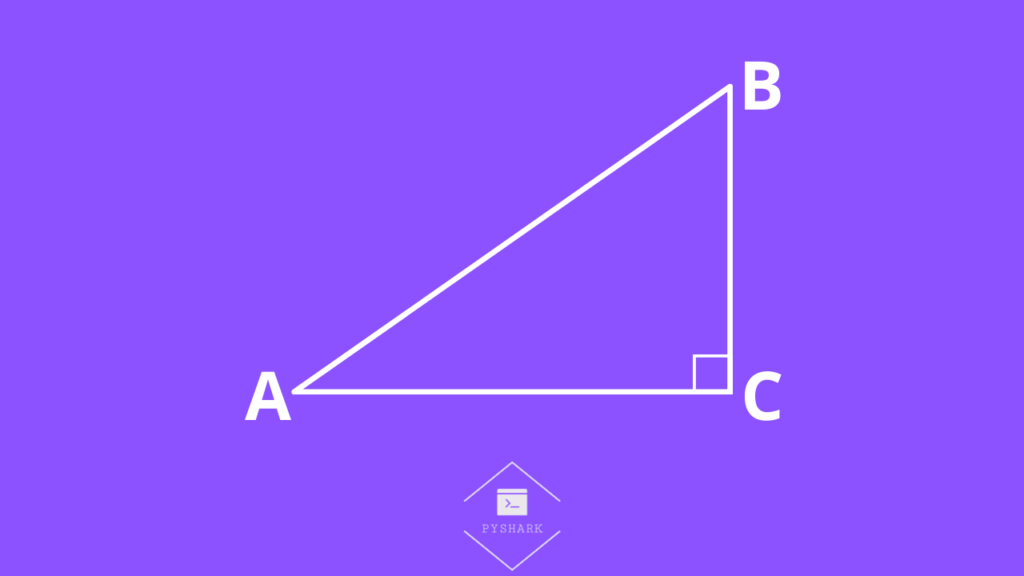
Here, angle C is the right angle (\(\angle C = 90^{\circ}\)), which now forms a right triangle ABC.
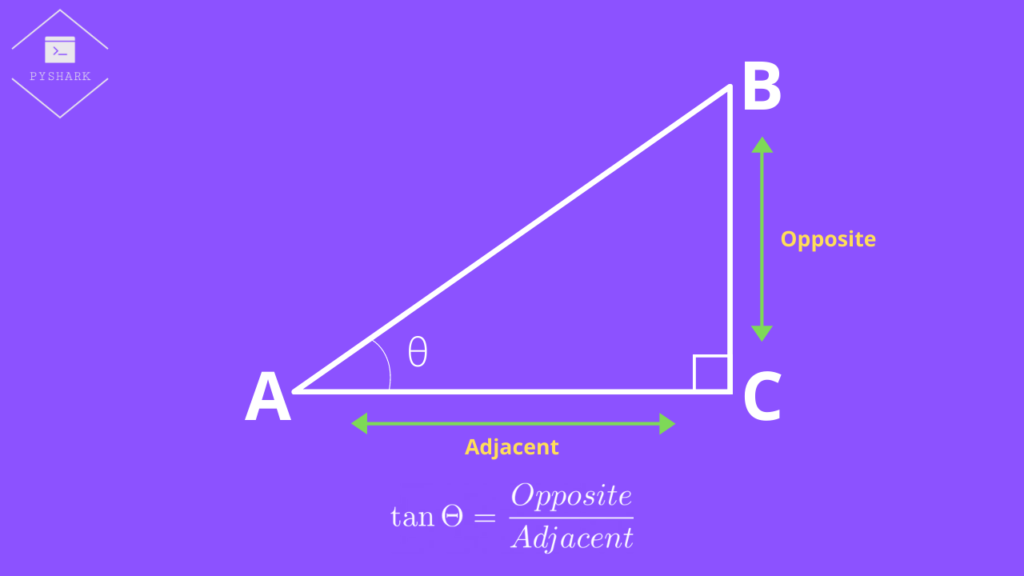
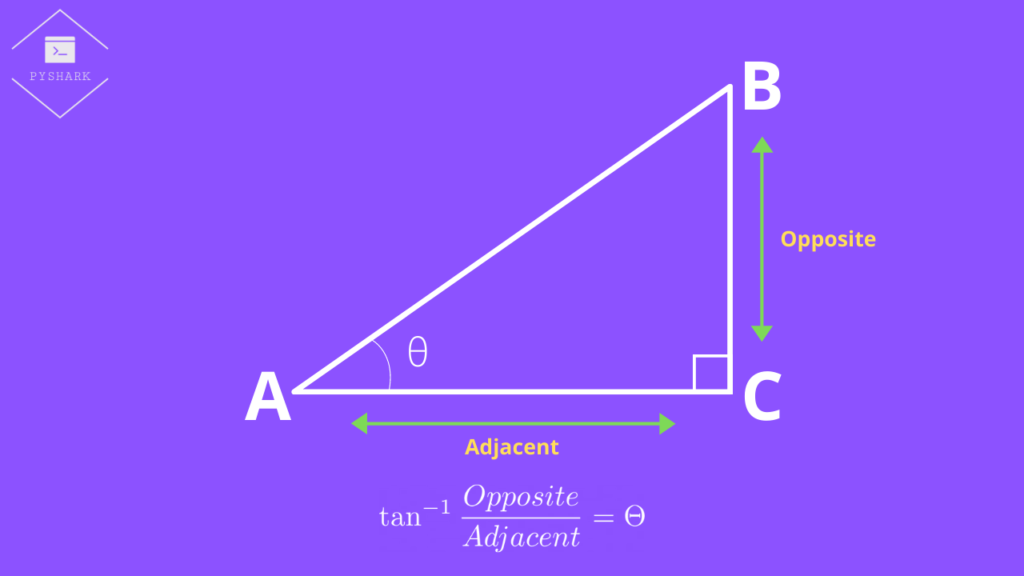
In addition, we should learn the names of the sides of the right triangle with respect to some chosen angle \(\Theta\).
See below:
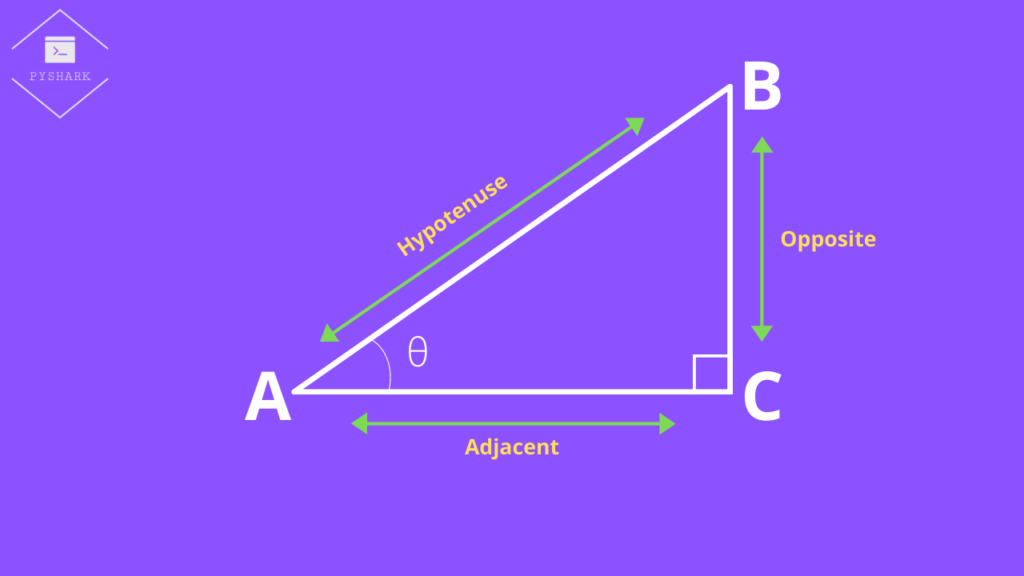
- Adjacent – the side always adjacent to the angle \(\Theta\) and also forms the right angle (\(90^{\circ}\)).
- Opposite – the side opposite of the angle \(\Theta\).
- Hypotenuse – the side opposite of the right angle (\(90^{\circ}\)) and also is the longest side in the right triangle.
Radian
Another important concept in geometry is radian. Radian is a unit of angle in the center of a circle which is created by the radius of the circle connected to an arc of an equal length with radius.
The formal definition sounds very complicated and challenging to follow, so it’s much easier to work through this definition visually.
See below:
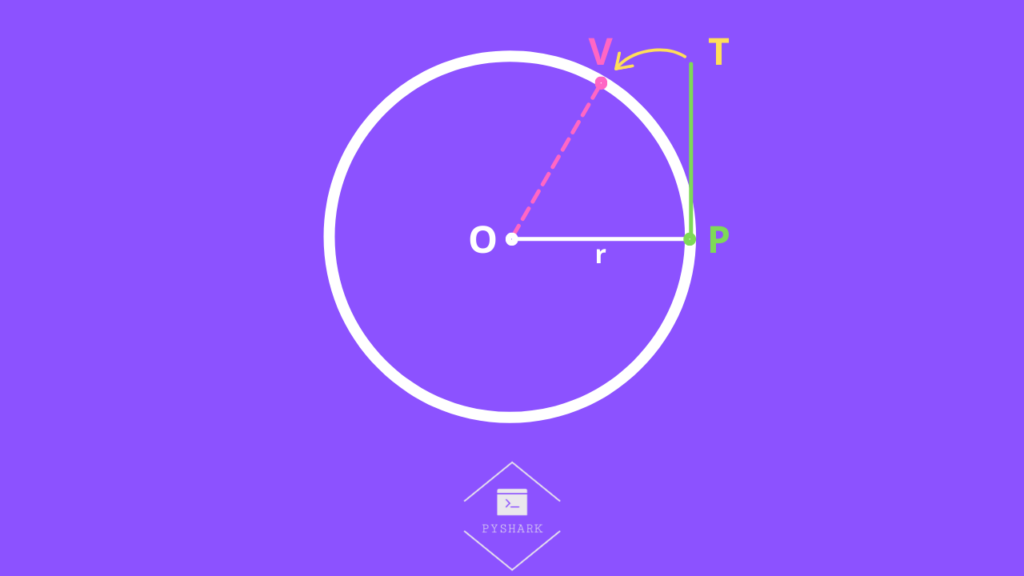
Step by step explanation:
- Start at point \(O\) and draw a horizontal line to point \(P\), which creates the segment \(OP\) with a length of a radius (\(r\)).
- From point P create a segment \(PT\) which is perpendicular to segment \(OP\) (angle = \(90^{\circ}\)), and is of the same length as segment \(OP\) which is equal to radius (\(r\)). You should have equal lengths: \(OP\)=\(PT\).
- Next, imagine you were to start bending the segment \(TP\) to the left until it fits the circumference. One you do it, you have a projection of segment \(TP\), which is an arc \(VP\). You should have equal lengths: \(TP\)=\(VP\).
After these steps, we have created an angle \(\angle VOP\) which is what we refer to as 1 radian:
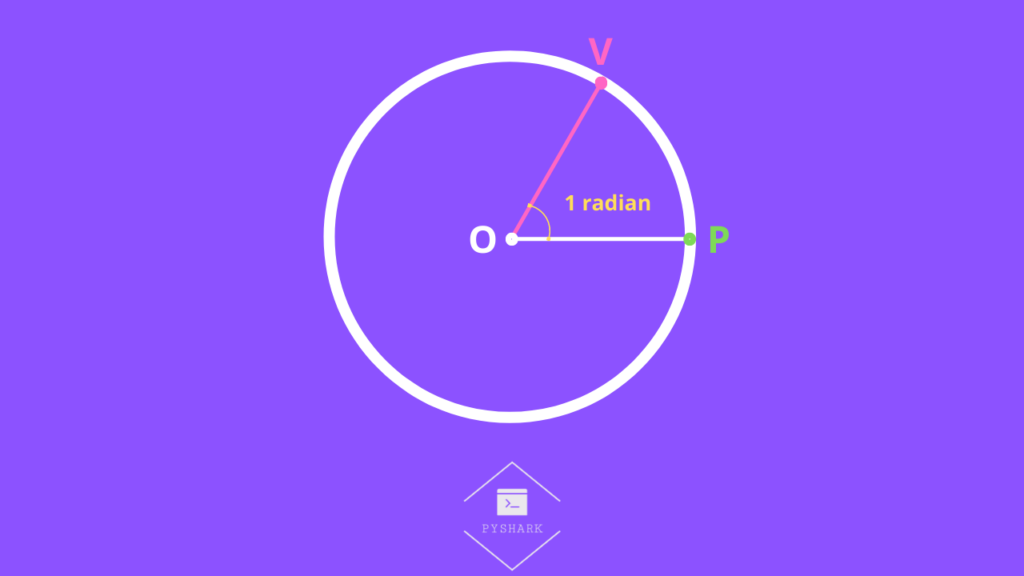
This angle is exactly 1 radian, or can also be calculated in degrees as:
$$1 \textit{ rad} = 1 \textit{ rad} \times \frac{180^{\circ}}{\pi} \approx 57.296^{\circ}$$
Alternatively, we can calculate degrees in radians:
$$1^{\circ} = 1^{\circ} \times \frac{\pi}{180^{\circ}} \approx 0.01745\textit{ rad}$$
Sine function
Sine function is one of the main trigonometric functions.
Sine function explained
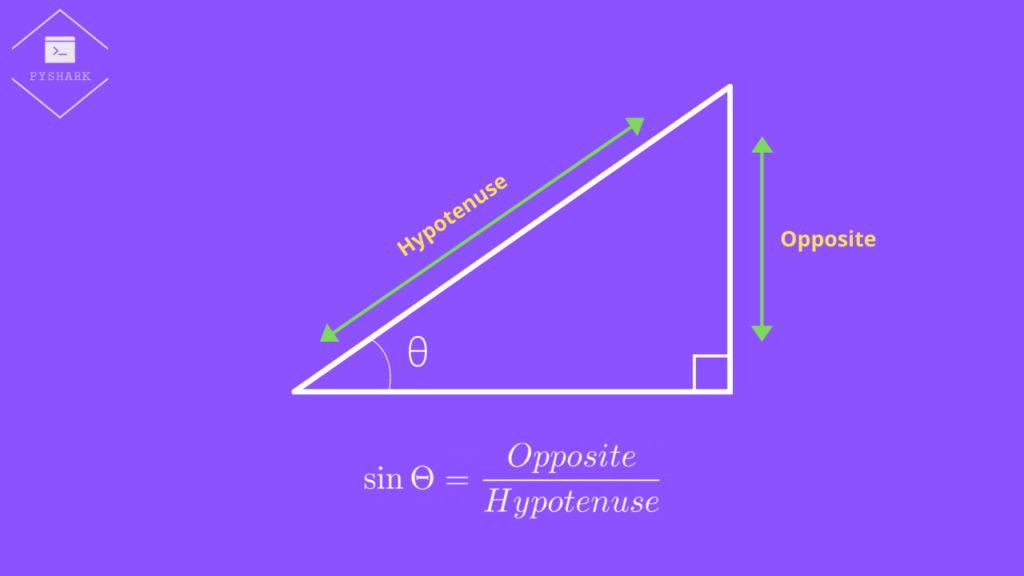
The sine function of angle \(\Theta\) is the ratio of the side of the triangle opposite the angle \(\Theta\) and the hypotenuse:
$$\sin \Theta = \frac{Opposite}{Hypotenuse}$$
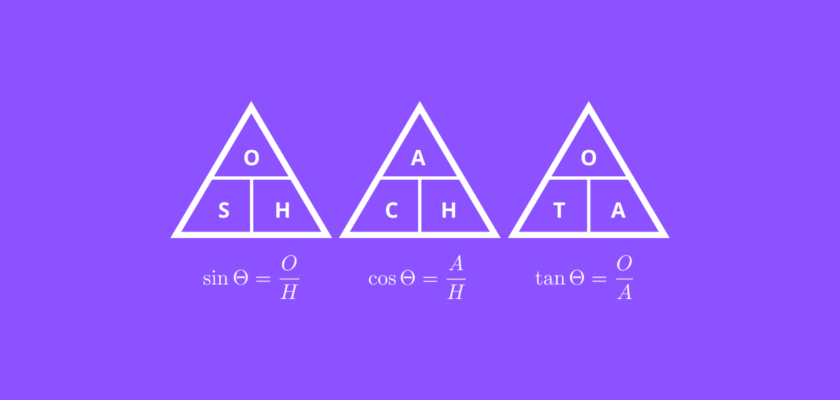
It is also often referred to as SOH: Sine is Opposite over Hypotenuse.
There is also a table that provides values of sine values for standard angles:
| Degrees | Radians | \(\sin \Theta\) |
| 30 | \(\frac{\pi}{6}\) | \(\frac{1}{2}\) |
| 45 | \(\frac{\pi}{4}\) | \(\frac{1}{\sqrt{2}}\) |
| 60 | \(\frac{\pi}{3}\) | \(\frac{\sqrt{3}}{2}\) |
Sine function calculation example
We have a right triangle \(ABC\), where \(AB\) = 20cm, \(\angle A = 30^{\circ}\), and \(\angle C = 90^{\circ}\) as shown in the figure below. We need to find the length of \(BC\).
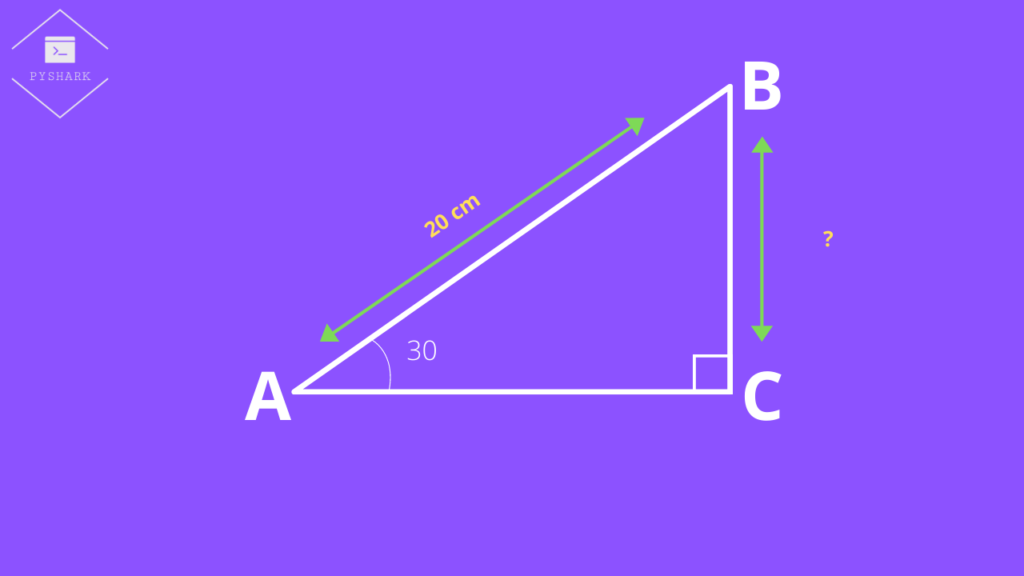
From the table in the previous section we know that \(\sin 30 = \frac{1}{2}\), and we can use this to solve the question in example:
$$\sin 30 = \frac{1}{2} = \frac{Opposite}{Hypotenuse} = \frac{BC}{AB} = \frac{BC}{20} \Longrightarrow BC = 10$$
In this example, using the \(\sin\) function we were able to find the length of side BC which is equal to 10 cm.
Sine function sin() in Python
In this section we will try to solve the above example using Python.
In order use the sine function sin() in Python we will need to import it from math library (which is built-in).
The input into sin() function should be in the format of radians, but in our example, we know that the angle is \(30^{\circ}\). We will need to convert degrees to radians using radians() also from math library.
Let’s begin with importing the required functions:
from math import sin, radians
Next, convert degrees into radians:
rad = radians(30)
And calculate the ratio (note that you should round it to 2 decimals):
ratio = sin(rad)
ratio = round(ratio, 2)
print(ratio)
And you should get:
0.5Which is exactly the same ratio of \(\sin 30\) as we saw in the previous section. We found the same result by using trigonometric functions in Python.
The rest of the calculations would be the same and you will get the answer equal to 10 cm.
Inverse sine function
Inverse sine function is one of the inverse trigonometric functions often referred to as arc sine.
Inverse sine function explained
The inverse sine function of the ratio of the side of the triangle opposite the angle \(\Theta\) and the hypotenuse is angle \(\Theta\).
It doesn’t sound as intuitive as it actually looks.
Recall that the sine function takes angle \(\Theta\) and gives the ratio of \(\frac{Opposite}{Hypotenuse}\).
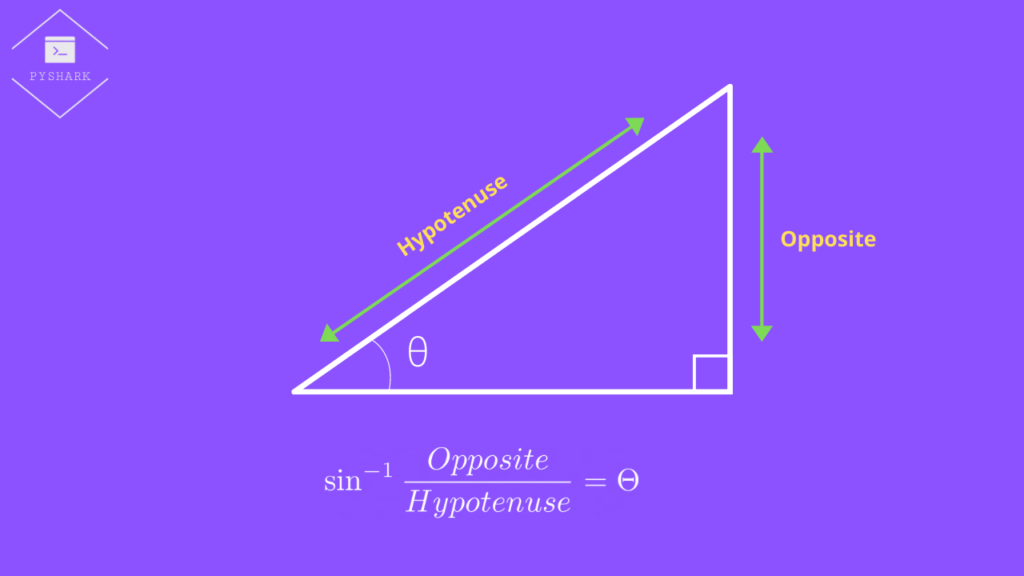
Now, the inverse sine function takes the ratio of \(\frac{Opposite}{Hypotenuse}\) and gives angle \(\Theta\):
$$\sin^{-1} \frac{Opposite}{Hypotenuse} = \arcsin \frac{Opposite}{Hypotenuse} = \Theta$$
Inverse sine function calculation example
We have a right triangle \(ABC\), where \(AB\) = 20cm, \(BC\) = 10cm, and \(\angle C = 90^{\circ}\) as shown in the figure below. We need to find \(\angle A\).
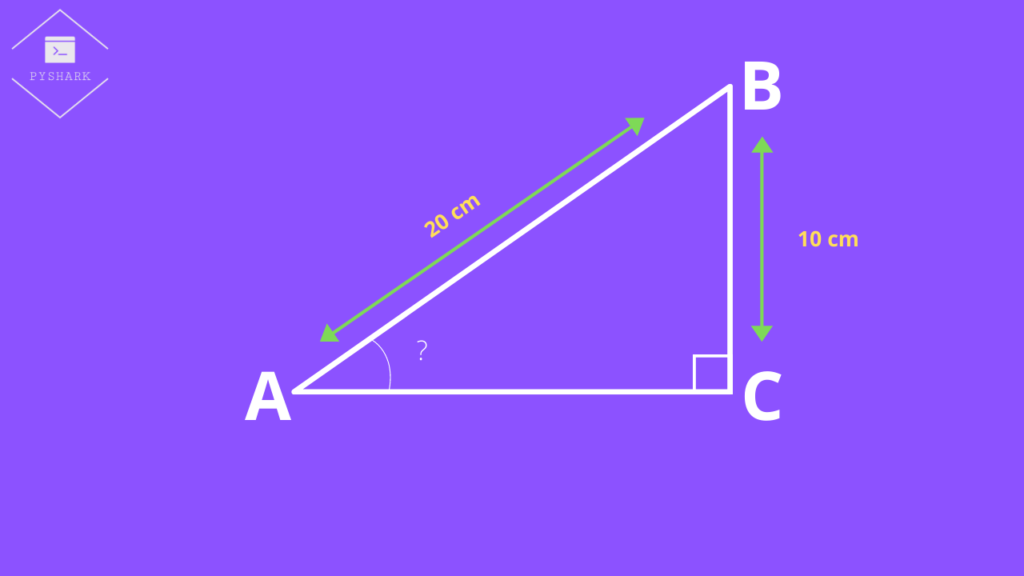
First, we will find the ratio of \(\frac{Opposite}{Hypotenuse}\):
$$\frac{Opposite}{Hypotenuse} = \frac{BC}{AB} = \frac{10}{20} = \frac{1}{2}$$
When we know the ratio, we can easily find the angle \(\Theta\) using any calculator and the arcsin function.
You should get:
$$\sin^{-1} \frac{1}{2} = 30^{\circ}$$
Inverse sine function asin() in Python
In this section we will try to solve the above example using Python.
In order use the inverse sine asin() function in Python we will need to import it from math library (which is built-in).
The output of the asin() function will be in the format of radians, but would like to have it in degrees. We will need to convert radians to degrees using degrees() also from math library.
Let’s begin with importing the required functions:
from math import asin, degrees
Next, find the radian measure of angle of a ratio equal to \(\frac{1}{2}\):
rad_angle = asin(0.5)
print(rad_angle)
And you should get:
0.5235987755982989Then finally convert the radian measure to degrees (and round it):
degree_angle = degrees(rad_angle)
degree_angle = round(degree_angle, 2)
print(degree_angle)
And you should get:
30We found that the inverse sine of a \(\frac{1}{2}\) ratio is angle equal to \(30^{\circ}\) by using trigonometric functions in Python.
Cosine function
Sine function is the second most popular trigonometric function.
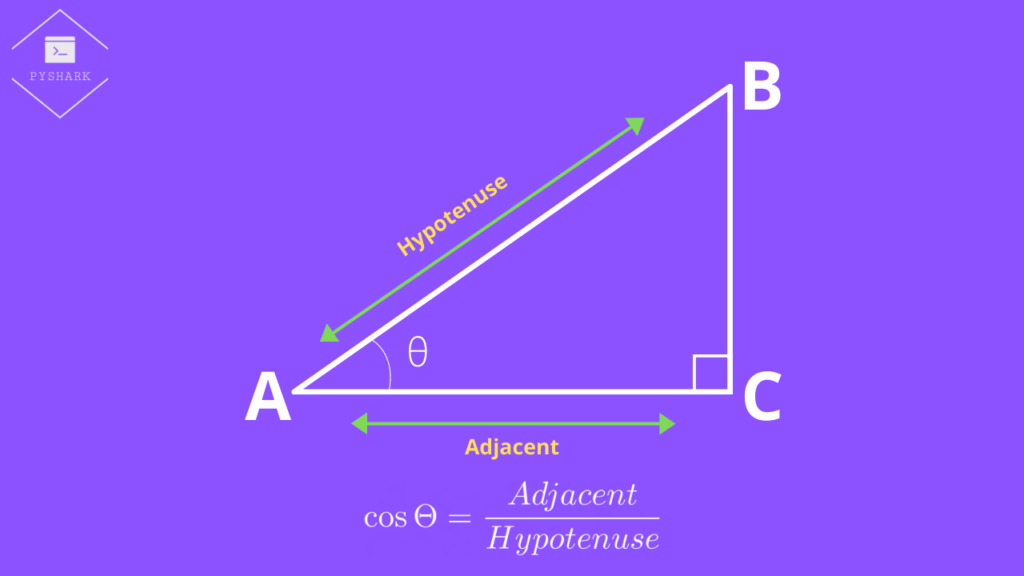
Cosine function explained
The cosine function of angle \(\Theta\) is the ratio of the side of the triangle adjacent to the angle \(\Theta\) and the hypotenuse:
$$\cos \Theta = \frac{Adjacent}{Hypotenuse}$$
It is also often referred to as CAH: Cosine is Adjacent over Hypotenuse.
There is also a table that provides values of cosine values for standard angles:
| Degrees | Radians | \(\cos \Theta\) |
| 30 | \(\frac{\pi}{6}\) | \(\frac{\sqrt{3}}{2}\) |
| 45 | \(\frac{\pi}{4}\) | \(\frac{1}{\sqrt{2}}\) |
| 60 | \(\frac{\pi}{3}\) | \(\frac{1}{2}\) |
Cosine function calculation example
We have a right triangle \(ABC\), where \(AB\) = 20cm, \(\angle B = 60^{\circ}\), and \(\angle C = 90^{\circ}\) as shown in the figure below. We need to find the length of \(BC\).
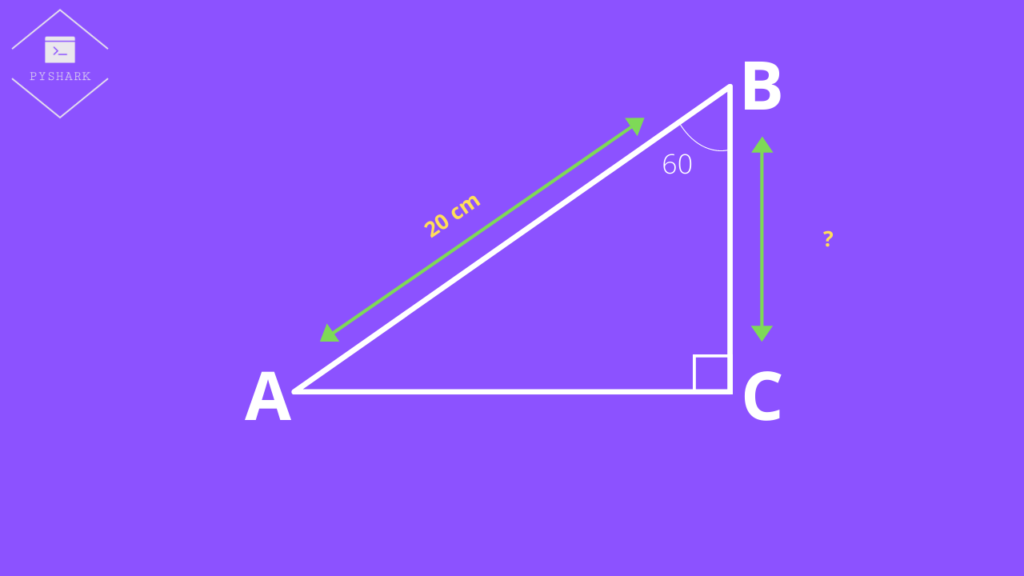
From the table in the previous section we know that \(\cos 60 = \frac{1}{2}\), and we can use this to solve the question in example:
$$\cos 60 = \frac{1}{2} = \frac{Adjacent}{Hypotenuse} = \frac{BC}{AB} = \frac{BC}{20} \Longrightarrow BC = 10$$
In this example, using the \(\cos\) function we were able to find the length of side BC which is equal to 10 cm.
Cosine function cos() in Python
In this section we will try to solve the above example using Python.
In order use the cosine function cos() in Python we will need to import it from math library (which is built-in).
The input into cos() function should be in the format of radians, but in our example, we know that the angle is \(60^{\circ}\). We will need to convert degrees to radians using radians() also from math library.
Let’s begin with importing the required functions:
from math import cos, radians
Next, convert degrees into radians:
rad = radians(60)
And calculate the ratio (note that you should round it to 2 decimals):
ratio = cos(rad)
ratio = round(ratio, 2)
print(ratio)
And you should get:
0.5Which is exactly the same ratio of \(\cos 60\) as we saw in the previous section. We found the same result by using trigonometric functions in Python.
The rest of the calculations would be the same and you will get the answer equal to 10 cm.
Inverse cosine function
Inverse cosine function is one of the inverse trigonometric functions often referred to as arc cosine.
Inverse cosine function explained
The inverse cosine function of the ratio of the side of the triangle adjacent to the angle \(\Theta\) and the hypotenuse is angle \(\Theta\).
Recall that the cosine function takes angle \(\Theta\) and gives the ratio of \(\frac{Adjacent}{Hypotenuse}\).
Now, the inverse cosine function takes the ratio of \(\frac{Adjacent}{Hypotenuse}\) and gives angle \(\Theta\):
$$\cos^{-1} \frac{Adjacent}{Hypotenuse} = \arccos \frac{Adjacent}{Hypotenuse} = \Theta$$
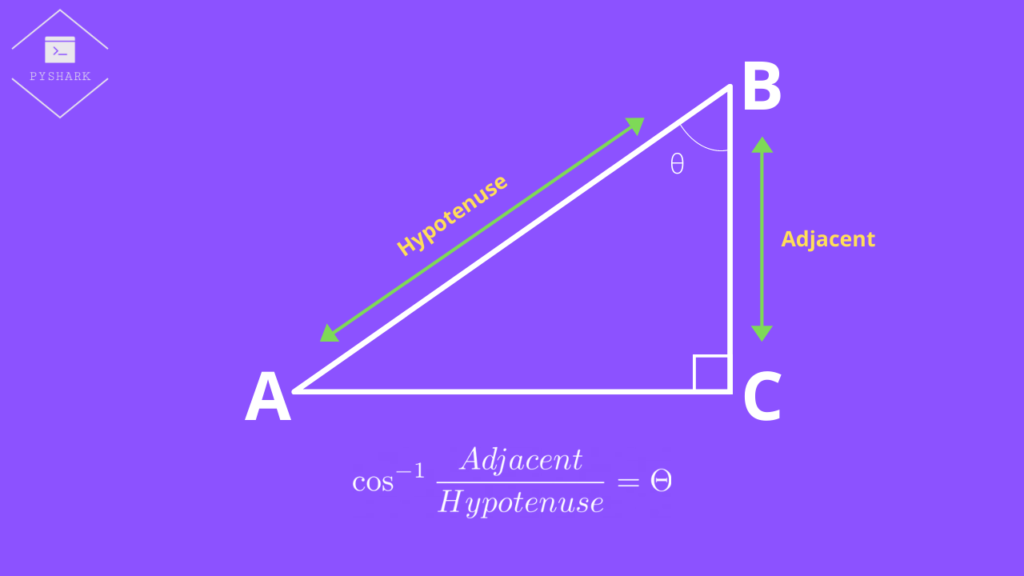
Inverse cosine function calculation example
We have a right triangle \(ABC\), where \(AB\) = 20cm, \(BC\) = 10cm, and \(\angle C = 90^{\circ}\) as shown in the figure below. We need to find \(\angle B\).
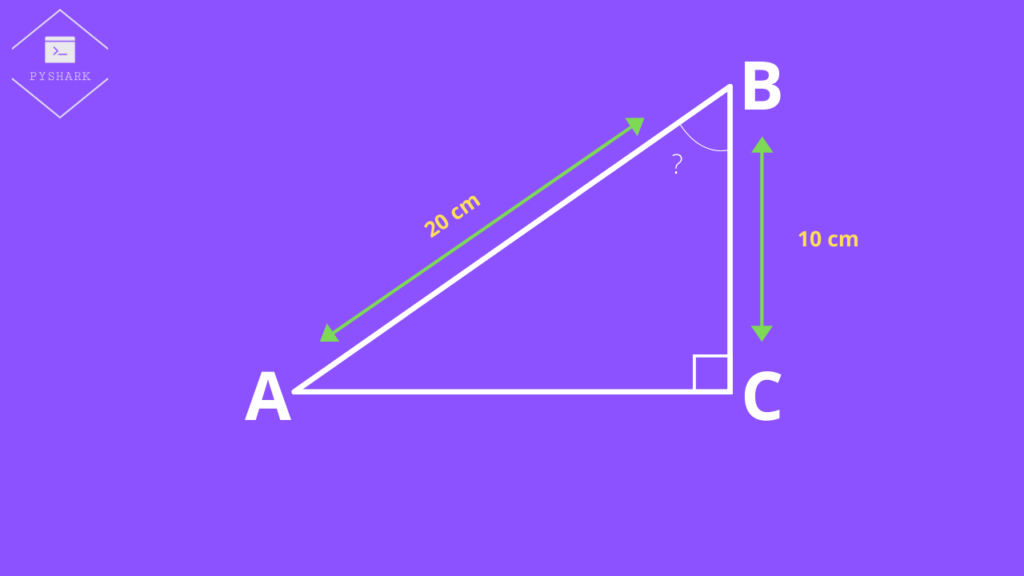
First, we will find the ratio of \(\frac{Adjacent}{Hypotenuse}\):
$$\frac{Adjacent}{Hypotenuse} = \frac{BC}{AB} = \frac{10}{20} = \frac{1}{2}$$
When we know the ratio, we can easily find the angle \(\Theta\) using any calculator and the arccos function.
You should get:
$$\cos^{-1} \frac{1}{2} = 60^{\circ}$$
Inverse cosine function acos() in Python
In this section we will try to solve the above example using Python.
In order use the inverse sine acos() function in Python we will need to import it from math library (which is built-in).
The output of the acos() function will be in the format of radians, but would like to have it in degrees. We will need to convert radians to degrees using degrees() also from math library.
Let’s begin with importing the required functions:
from math import acos, degrees
Next, find the radian measure of angle of a ratio equal to \(\frac{1}{2}\):
rad_angle = acos(0.5)
print(rad_angle)
And you should get:
1.0471975511965979Then finally convert the radian measure to degrees (and round it):
degree_angle = degrees(rad_angle)
degree_angle = round(degree_angle, 2)
print(degree_angle)
And you should get:
60.0We found that the inverse cosine of a \(\frac{1}{2}\) ratio is angle equal to \(60^{\circ}\) by using trigonometric functions in Python.
Tangent function
Tangent function is the third popular trigonometric function.
Tangent function explained
The tangent function of angle \(\Theta\) is the ratio of the side of the triangle opposite to the angle \(\Theta\) and the side of the triangle adjacent to the angle \(\Theta\):
$$\tan\Theta = \frac{Opposite}{Adjacent}$$
It is also often referred to as TOA: Tangent is Opposite over Adjacent.
There is also a table that provides values of tangent values for standard angles:
| Degrees | Radians | \(\tan \Theta\) |
| 30 | \(\frac{\pi}{6}\) | \(\frac{1}{\sqrt{3}}\) |
| 45 | \(\frac{\pi}{4}\) | \(1\) |
| 60 | \(\frac{\pi}{3}\) | \(\sqrt{3}\) |
Tangent function calculation example
We have a right triangle \(ABC\), where \(BC\) = 10cm, \(\angle A = 30^{\circ}\), and \(\angle C = 90^{\circ}\) as shown in the figure below. We need to find the length of \(AC\).
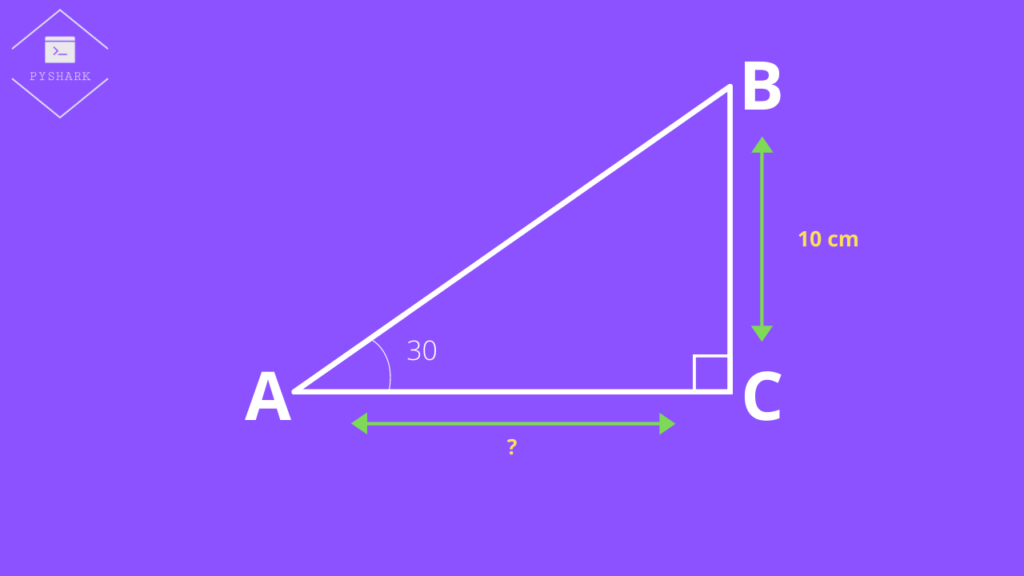
From the table in the previous section we know that \(\tan 30 = \frac{1}{\sqrt{3}}\), and we can use this to solve the question in example:
$$\tan 30 = \frac{1}{\sqrt{3}} = \frac{Opposite}{Adjacent} = \frac{BC}{AC} = \frac{10}{AC} \Longrightarrow BC = 10\sqrt{3} \approx 17.32$$
In this example, using the \(\tan\) function we were able to find the length of side BC which is equal to 17.32 cm.
Tangent function tan() in Python
In this section we will try to solve the above example using Python.
In order use the tangent function tan() in Python we will need to import it from math library (which is built-in).
The input into tan() function should be in the format of radians, but in our example, we know that the angle is \(30^{\circ}\). We will need to convert degrees to radians using radians() also from math library.
Let’s begin with importing the required functions:
from math import tan, radians
Next, convert degrees into radians:
rad = radians(30)
And calculate the ratio (note that you should round it to 2 decimals):
ratio = tan(rad)
ratio = round(ratio, 2)
print(ratio)
And you should get:
0.58In this case, the ratio is 0.58 which is approximately equal to \(\frac{1}{\sqrt{3}}\), which is exactly the same ratio of \(\tan 30\) as we saw in the previous section. We found the same result by using trigonometric functions in Python.
The rest of the calculations would be the same and you will get the answer equal to 17.24 cm (whereas the calculated without rounding would be 17.32 cm).
Inverse tangent function
Inverse tangent function is one of the inverse trigonometric functions often referred to as arc tangent.
Inverse tangent function explained
The inverse tangent function of the ratio of the side of the triangle opposite to the angle \(\Theta\) and the side of the triangle adjacent to the angle \(\Theta\).
Recall that the tangent function takes angle \(\Theta\) and gives the ratio of \(\frac{Opposite}{Adjacent}\).
Now, the inverse tangent function takes the ratio of \(\frac{Opposite}{Adjacent}\) and gives angle \(\Theta\):
$$\tan^{-1} \frac{Opposite}{Adjacent} = \arccos \frac{Opposite}{Adjacent} = \Theta$$
Inverse tangent function calculation example
We have a right triangle \(ABC\), where \(BC\) = 10 cm, \(AC\) = 17.32 cm, and \(\angle C = 90^{\circ}\) as shown in the figure below. We need to find \(\angle B\).
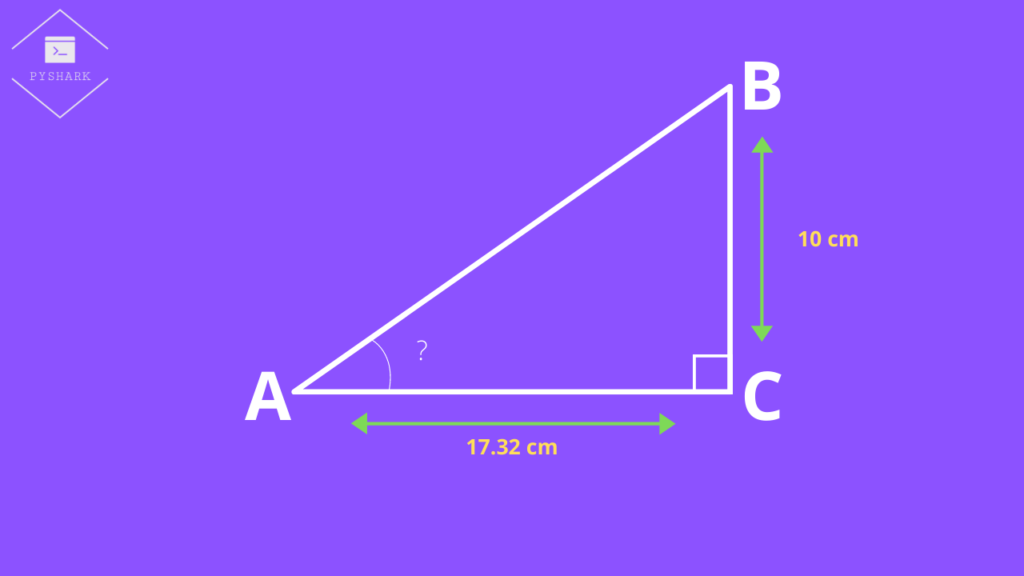
First, we will find the ratio of \(\frac{Opposite}{Adjacent}\):
$$\frac{Opposite}{Adjacent} = \frac{BC}{AC} = \frac{10}{17.32} \approx 0.58$$
When we know the ratio, we can easily find the angle \(\Theta\) using any calculator and the arctan function.
You should get:
$$\tan^{-1} 0.58 \approx 30^{\circ}$$
Inverse tangent function atan() in Python
In this section we will try to solve the above example using Python.
In order use the inverse sine atan() function in Python we will need to import it from math library (which is built-in).
The output of the acos() function will be in the format of radians, but would like to have it in degrees. We will need to convert radians to degrees using degrees() also from math library.
Let’s begin with importing the required functions:
from math import atan, degrees
Next, find the radian measure of angle of a ratio equal to \(0.58\):
rad_angle = atan(0.58)
print(rad_angle)
And you should get:
0.5255837935516101Then finally convert the radian measure to degrees (and round it):
degree_angle = degrees(rad_angle)
degree_angle = round(degree_angle, 2)
print(degree_angle)
And you should get:
30.11We found that the inverse cosine of a \(0.58\) ratio is angle equal to \(30.11^{\circ}\) by using trigonometric functions in Python, which is approximately equal to \(30^{\circ}\) if we didn’t have the length of side \(AC\) rounded to 17.32 cm.
Conclusion
In this article we will focused on a complete walkthrough of trigonometric functions in Python using functions from math library. It includes sine, cosine, tangent, inverse sine, inverse cosine, and inverse tangent.
Feel free to leave comments below if you have any questions or have suggestions for some edits and check out more of my Statistics articles.